Valószínűség számítás 1.

Egy 100 fős évfolyamon 56 lány és 44 fiú van. Kiválasztunk az évfolyamból egy 10 fős mintát és a fiúk számával fogunk vizsgálatokat folytatni (jelölje őket X).

a. Számítsa ki az alábbi valószínűségeket, ha a mintát visszatevés nélkül vesszük!

P(X=3)

P(X<=3)

P(X<3)

P(X>=3)

P(X>3)

P(4<=X<=7)

P(4<=X<7)

 Visszatevés nélkül, tehát ugyanaz a lány és ugyanaz a lány nem kerülhet bele kétszer a mintába.

P(X=3) azt jelenti, hogy a 10 főből 3 a fiú. Számoljuk ki Excel segítségével, mennyi ennek a valószínűsége!

Írjuk fel az adatokat:

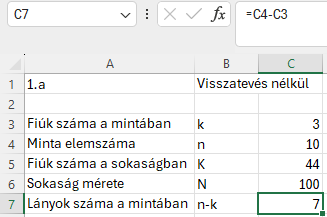
P(X=3)

Fiúk száma a mintában: k=3

Minta elemszáma:          n=10

Fiúk száma a sokaságban: K=44

Sokaság mérete:             N=100

Lányok száma a mintában: n-k=7

Lányok száma a sokaságban: N-K=56

Összes eset száma: 

N alatt a n, 100 alatt a 10

A KOMBINÁCIÓK függvénnyel kiszámolva:

Kedvező esek:

K alatt a k , szorozva N-K alatt a n-k

44 alatt a 3 , szorozva 56 alatt a 7

Valószínűség P(X=3)

Kedvező eset osztva az összes esettel:

Tehát 17,74% a valószínűsége, hogy a 10 főből 3 fiú lesz a mintában.

Ez alapján ki tudjuk számolni, ha a fiúk száma 0,1...10. A lányok száma is változik, ezért azt is ki kell számolni.

Ezek alapján a kedvező esetek:

A fiúk száma a sokaságban (K),  a lányok száma a sokaságban (N-K) nem változik, lezárjuk F4-gyel.

Változik a fiúk száma a mintában (k), a lányok száma a mintában (n-k)

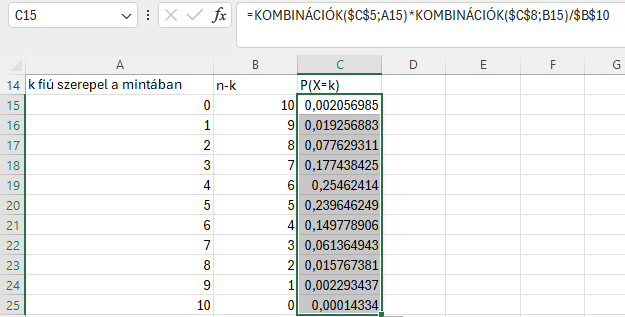
=KOMBINÁCIÓK($C$5;A15)*KOMBINÁCIÓK($C$8;B15)

Ahhoz, hogy a valószínűséget megkapjuk az összes esettel el kell osztani a megkapott számot.

=KOMBINÁCIÓK($C$5;A15)*KOMBINÁCIÓK($C$8;B15)/$B$10 , az összes eset változatlan, tehát le kell zárni F4-gyel.

Eredmény:

P(X<=3) 

Annak, hogy 3 vagy kevesebb fiú van a mintában, a valószínűsége:

Összeadjuk a 0-3-ig valószínűséget, és megkapjuk, hogy 27,64% a valószínűsége, hogy 3 vagy kevesebb fiú lesz a mintában.

P(X<3) 

Összeadjuk a 0-2-ig valószínűséget, és megkapjuk, hogy 9,89% a valószínűsége, hogy kevesebb, mint 3 fiú lesz a mintában.

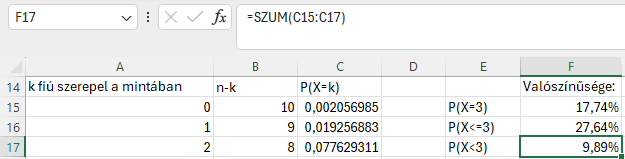
P(X>=3)

Összeadjuk a 3-10-ig valószínűséget, és megkapjuk, hogy 90,11% a valószínűsége, hogy 3 vagy több fiú lesz a mintában.

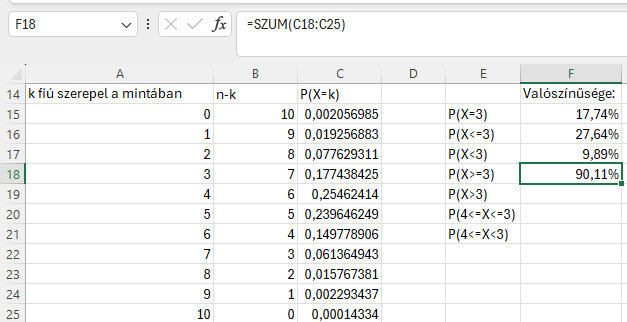
P(X>3)

Összeadjuk a 4-10-ig valószínűséget, és megkapjuk, hogy 72,36% a valószínűsége, hogy több mint 3 fiú lesz a mintában.

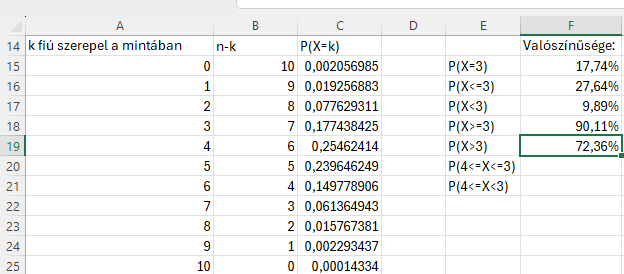
P(4<=X<=7)

Összeadjuk a 4-7-ig valószínűséget, és megkapjuk, hogy 70,54% a valószínűsége, hogy 4 és 7 között lesz a fiúk száma a mintában.

P(4<=X<7)

Összeadjuk a 4-6-ig valószínűséget, és megkapjuk, hogy 64,40% a valószínűsége, hogy 4 és 6 között lesz a fiúk száma a mintában.