Valószínűség számítás 2. Visszatevés

Egy 100 fős évfolyamon 56 lány és 44 fiú van. Kiválasztunk az évfolyamból egy 10 fős mintát és a fiúk számával fogunk vizsgálatokat folytatni (jelölje őket X).

 b. Számítsa ki az alábbi valószínűségeket, ha a mintát visszatevéssel vesszük!

P(X=3)

P(X<=3)

P(X<3)

P(X>=3)

P(X>3)

P(4<=X<=7)

P(4<=X<7)

P(X=3) azt jelenti, hogy a 10 főből 3 a fiú. Számoljuk ki Excel segítségével, mennyi ennek a valószínűsége!

Írjuk fel az adatokat:

 P(X=3)

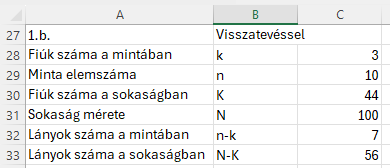
Fiúk száma a mintában: k=3

Minta elemszáma:          n=10

Fiúk száma a sokaságban: K=44

Sokaság mérete:             N=100

Lányok száma a mintában: n-k=7

Összes eset: N felemelve a n.-re

=C31^C29  (^ AltGr+3, majd szóköz) 100 felemelve a 10.-re.

Kedvező esetek száma:

(n alatt a k )* K^k*(N-K)^(n-k)

(10 alatt a 3)*44^3*56^7

Képlet:

=KOMBINÁCIÓK($C$29;C28)*$C$30^C28*$C$33^C32

Rögzítve (F4) az n; K; N-K, mivel másolásnál ezek nem változhatnak.

Valószínűsége, hogy X=3: Kedvező esetek száma/Összes eset száma:

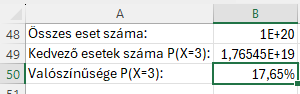
Hasonló az előző példához az eredmény.

Nézzük meg a 11 féle variációt, melyiknek mennyi a valószínűsége:

Ha ezt az összes valószínűséget összeadom, akkor 1-et kell kapnom, mivel az összes lehetséges esetet felsoroltuk.

=SZUM(C36:46) eredmény:

Ezek alapján a valószínűségek táblázata:

 Egyszerűen összeadjuk a megfelelő valószínűségeket: Ha x<=3, akkor a (k=0)+(k=1)+(k=2)+(k=3) valószínűségeit összeadjuk.