Valószínűségszámítás 3. Feltételes

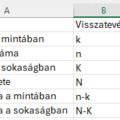
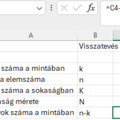
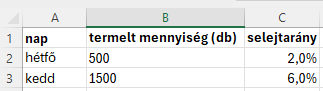
5. Két napon egy gyárban azonos termékeket gyártanak (más napokon nincs gyártás). A napi termelt mennyiségek és selejtarányok az alábbi táblázatban találhatók:

Legyen A="A termék hibás", illetve H= "Hétfői termelés". Határozza meg a P(H), P(A), 

, ,  

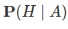
valószínűségeket!

Annak a valószínűsége, hogy hétfőn gyártották a terméket:

a, P(H)

Valószínűség kiszámítása: A hétfői termelést (500) el kell osztani a teljes termeléssel (2000).

Tehát 0,25 (25%)  a valószínűsége, hogy a hétfői termelésben volt hibás termék.

P(H)=0,25

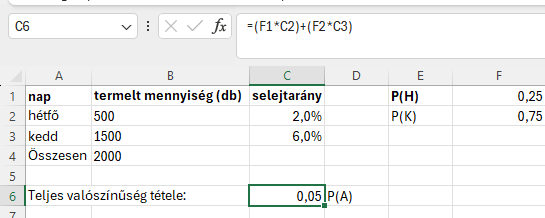
 b, P(A) annak a valószínűsége, hogy a kiválasztott termék hibás:

Hétfőn 2,0 % volt a hibás, kedden meg 6,0%. Ezekből súlyozott átlagot kell számolni.

 Teljes valószínűség tétel:

(Hétfői valószínűséget megszorozzuk a hétfői selejttel) + (annak a valószínűsége, hogy kedden lett hibás megszorozzuk a keddi selejttel)

P(A)=0,05

c,  vagyis az a, esemény komplementere. Annak valószínűsége, hogy nem hibás a termék.

P(A fv.)=1-P(A)=1-0,05=0,95

d,  =0,02

Mi a valószínűsége, hogy a termék hibás, és hétfőn gyártották.

Táblázatban szerepel, ha hétfőn gyártották, akkor 2,0% a valószínűsége, hogy hibás.

e,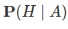

Ha tudjuk, hogy a termék hibás, akkor annak mi a valószínűsége, hogy hétfőn gyártották. 

 * P(H)  egész osztva P(A) 

Tehát (0,02*0,25)/0,05=0,1

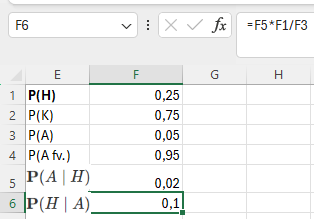
 10 százalék annak a valószínűsége, ha tudjuk, hogy hibás, akkor hétfőn gyártották.