Kollégium 2.MIN ; ÁTLAG ; HA

A Kocka Kollégiumban kis csoportokban foglalkoznak a kollégistákkal. Az egyes csoportokat színekkel azonosítják. A félévi értesítők kiosztását követően minősítik a csoportokat  a diákok átlagai alapján, valamint az intézmény honlapján megjelentetik a statisztikai adatokat. Az alábbi feladatban ezt kell elkészítenie.

2. A T oszlopban határozza meg az egyes diákok tanulmányi átlageredményét! Egy tanuló tanulmányi átlaga 1, ha bármely tárgyból elégtelen osztályzatot kapott, egyébként pedig a jegyek számtani közepe.

 Fontos feltétel, hogy ha van elégtelen osztályzata bármely tantárgyból, akkor az átlageredménye : 1.

Nézzük meg minden gyereknél melyik a legkisebb osztályzata a MIN függvénnyel.

 MIN - Egy értékhalmazban lévő legkisebb számot adja meg. A logikai értékeket és a szövegeket figyelmen kívül hagyja

Képlete:

 =MIN(szám1;szám2;....szám255)

szám1;szám2;....szám255  -  F2:S2 cellatartományon beül vizsgálja meg, melyik a legkisebb érdemjegy

Képlete:

=MIN(F2:S2)

A következő feltétel, ha nincs elégtelenje, akkor a tanulmányi átlagot írja ki, melyet az ÁTLAG függvénnyel számoltatunk ki.

ÁTLAG - Argumentumainak átlagát (számtani közepét) számítja ki, az argumentumok nevek, tömbök vagy számokat tartalmazó hivatkozások lehetnek.

Képlete:

=ÁTLAGA(érték_1;érték_2;...)

érték_1;érték_2;... - A tantárgyi érdemjegyek : F2:S2

Képlete:

=ÁTLAG(F2:S2)

Ahhoz, hogy épp melyik változat kerüljön az adott cellába a HA logikai függvényt fogjuk használni.

HA(logikai vizsgálat (kötelező); érték, ha igaz ( kötelező); érték, ha hamis (nem kötelező)) 

 logikai vizsgálat - vizsgálja meg, hogy melyik a legkisebb érdemjegy, és egyenlő e 1-gyel : MIN(F2:S2)=1

érték, ha igaz - írja ki "1"

érték, ha hamis - nézze meg a tanulmányi átlagot az előzőekben meghatározott ÁTLAG függvénnyel : ÁTLAG(F2:S2)

Képlet:

=HA(MIN(F2:S2)=1;1;ÁTLAG(F2:S2))

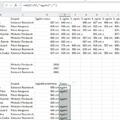
Eredmény:

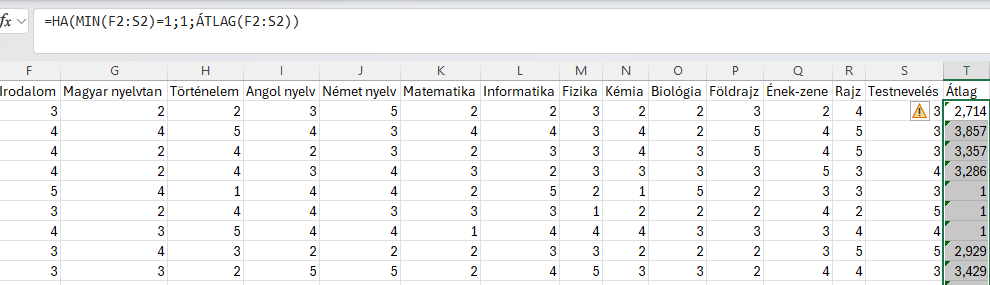
Hogyan oldanád meg?

3. Az U oszlopban minősítse a diákokat átlaguk alapján! A 2,00 alatti átlag minősítése elégtelen, 2,00-tól elégséges, 2,75-től közepes, 3,75-től jó, 4,50-től jeles, az 5,00 pedig a kitűnőnek felel meg. A feladat megoldásánál – ha szükségesnek látja – segédcellákat használhat és segédszámításokat végezhet.